Arabische wiskunde

Inhoudsopgave

Klik op de regel en je scrollt meteen naar het onderwerp in kwestie.

Inleiding

Op deze pagina hebben we het over de wiskunde van de Arabieren. Na de dood van Mohammed (622) namen de Arabieren de overheersende positie van de Grieken in de landen rond de Middellandse Zee over. Ze waren gelukkig niet afkerig van de cultuur van hun voorgangers, maar deden juist hun best om die zo volledig mogelijk over te nemen. Veel Griekse teksten werden in het Arabisch vertaald, en op die manier leefde de Griekse wiskundige kennis bij de Arabieren voort. Na enkele eeuwen begonnen ze de Griekse wetenschap ook zelf verder te ontwikkelen. Een goed voorbeeld van een Arabische wiskundige die nieuwe wiskunde ontworpen heeft is Al-Chwarizmi.

Video – Al Khwarizmi
In deze video wordt in het Engels uitgelegd wie Al-Chwarizmi is en wat hij bijgedragen aan de moderne algebra.

Video – Oorsprong van Algebra
In deze video wordt in het Engels (Nederlandse ondertiteling aanwezig) vertelt over de oorsprong van Algebra.

Hieronder volgt een vertaling van een stukje uit de Hisab al-jabr wal-moeqabala van Al-Chwarizmi. Dit stukje wordt ook behandeld in bovenstaande video. Hij lost erin de vergelijking x² + 10x = 39 op.

“Een kwadraat en tien keer zijn wortel vormen samen negenendertig eenheden. Dit wil zeggen: welk getal moet gekwadrateerd worden zodat het kwadraat plus tien keer het getal, negenendertig oplevert? De oplossing is:
Neem de helft van (in dit geval) tien, en vermenigvuldig dit met zichzelf, dus je krijgt: vijf keer vijf is vijfentwintig. Dit product wordt bij negenendertig opgeteld, de som is vierenzestig. Neem hiervan de wortel, dit is acht. Trek van acht de helft van (in dit geval) tien af. De rest is drie. Dit is de wortel van het getal dat je aan het boeken bent. Het kwadraat zelf is negen.”

Meetkundige toelichting:  ax² + bx = c

Voorbeeld: x² + 10x = 39

  • Je tekent een vierkant met onbekende zijde. Deze zijde noem je x. De oppervlakte van dit vierkant is dus x².
  • Vervolgens teken je 10x. Dit doe je door een rechthoek te tekenen, waarvan één zijde gelijk aan x is en de andere zijde gelijk aan 10 (zie het linker figuur hieronder). De vergelijking vertelt ons dat de oppervlakte van deze hele figuur gelijk is aan 39.
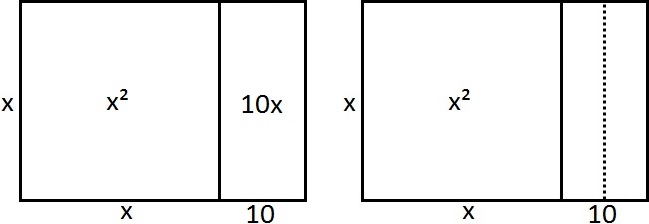
  • Hierna verdeel je het gemaakte rechthoek in twee gelijke delen, elk met oppervlakte 5x (zie het rechter figuur hierboven).
  • Nu verplaats je één van de halve rechthoeken naar de onderkant van het vierkant (zie het linker figuur hieronder). De totale oppervlakte is nog steeds gelijk aan 39.
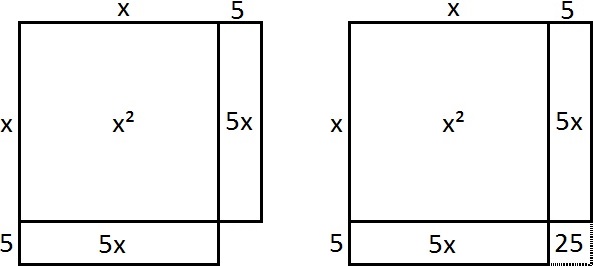
  • Rechtsonder voegen we nu een klein vierkantje toe, daardoor hebben we een groot vierkant gekregen. Omdat de twee rechthoeken zijde 5 hebben, is de oppervlakte van het kleine vierkantje gelijk aan 25 (zie het rechter figuur hierboven).
  • De oppervlakte van het grote vierkant is 39 + 25 = 64. Daar uit volgt dat de zijden van het grote vierkant gelijk is aan de wortel van 64, oftewel 8. De zijde van het grote vierkant is ook gelijk aan x + 5. Hier uit volgt dat x + 5 =8, dus x = 3.

Oefening 1
a. Bereken zelf de positieve oplossing van de vergelijking x² + 10x = 39 met behulp van de abc-formule. Welke overeenkomsten zie je met de berekening van Al-Chwarizmi?
b. Los nu op dezelfde meetkundige wijze, als Al-Chwarizmi, de volgende vergelijking op x² + 12x = 28.

Antwoordblad

Herkomst woorden ‘Algebra’ en ‘Algoritme’

Zoals je misschien al in het boek van Berlinghoff hebt gelezen of in de video aan het begin van deze pagina hebt gezien, komt het woord algebra van ‘al-jabr‘, dit is het eerst deel van de titel van een boek over het oplossen van vergelijkingen (Hisab al-jabr wal-moeqabala van Al-Chwarizmi).
Algoritme komt van Al-Chwarizmi. Het betekent zoiets als ‘recept’, ‘voorschrift’, ‘werkwijze’.

Verschil Arabische aanpak en onze huidige aanpak

Een groot verschil vergeleken met onze aanpak van vierkantsvergelijkingen is dat wij als coëfficiënten en oplossingen ook negatieve getallen toelaten. Al-Chwarizmi gebruikte die nog niet, en vond dus bij de vergelijking x² + 10x = 39 geen negatieve oplossingen (voor ons is die er wel: -13). Daardoor konden vierkantsvergelijkingen ook niet in één algemene vorm geschreven worden (zoals onze ax² + bx + c = 0), want in het linker- en het rechterlid moesten positieve getallen staan, en daarom moest Al-Chwarizmi wel drie verschillende typen onderscheiden:

  • ax² + bx = c (daarvan hebben we al een voorbeeld gezien)
  • ax² + c = bx
  • ax² = bx + c

Elk type had een eigen oplossingsmethode en die verschilden nogal van elkaar.

Meetkundige toelichting:  ax² + c = bx

Voorbeeld: x² + 21 = 10x

“Een kwadraat en éénentwintig eenheden vormen samen tien keer zijn wortel. Neem de helft van tien en vermenigvuldig dit met zichzelf. Trek van het nu gevonden getal éénentwintig af. Er blijft dan vier over. Neem de wortel van vier, deze wordt van vijf afgetrokken. Je hebt de eerste oplossing gevonden, namelijk: vijf min twee is gelijk aan drie. De tweede oplossing vind je door twee bij vijf op te tellen. Vijf plus twee is gelijk aan zeven.”

Om dit recept te begrijpen kijken we weer naar de meetkundige toelichting van Al-Chwarizmi. Hij begint met het vierkant ABDG te construeren (AG = x).

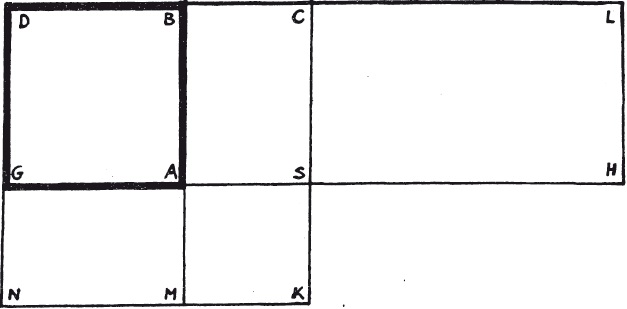
Aan dit vierkant wordt een rechthoek ABHL met oppervlakte 21 geplakt. Van deze rechthoek neemt Al-Chwarizmi eerst aan dat hij groter is dan vierkant ABDG. Hij gaat er dus van uit dat BL langer is dan BD.
De oppervlakte van ABDG en ABHL zijn samen gelijk aan x² + 21 en wegens de vergelijking is dit gelijk aan 10x. Dit betekent dat LD gelijk is aan 10. Laat punt C het midden van lijnstuk LD zijn. C ligt rechts van B. Dit betekent dat DC en CL gelijk zijn aan 5.
Construeer nu op lijnstuk DC het vierkant NKCD. Trek lijnstuk AB door totdat het KN snijdt in M. Verder is S het snijpunt van AH en CK.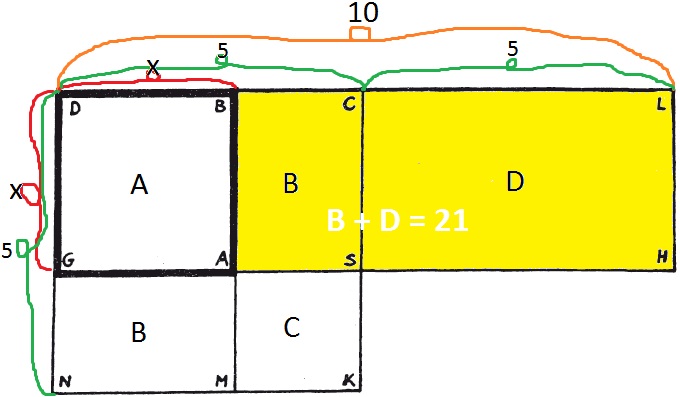

Uit bovenstaande afbeelding volgt:
A + B = D
A + 2B = D + B = 21
A + 2B + C = 21 + C
25 = 21 + C, dus C = 4
Elke ribbe van vierkant C is dus gelijk aan 2. Daaruit volg x + 2 = 5, dus x = 3.

In deze meetkundige toelichting nam Al-Chwarizmi aan dat BL langer was dan BD. We zullen hier geen aandacht besteden aan het geval dat BL kort is dan BD. Wil je hier wel de uitwerking van zien? Klik dan hier.

Oefening 2
Los nu op dezelfde meetkundige wijze, als Al-Chwarizmi, de volgende vergelijking op  x² + 27 = 12x (met x² < 27).

Antwoordblad

Extra oefening
Los de vergelijking, x² + 27 = 12x, op met x² > 27. Op dezelfde meetkundige wijze, als Al-Chwarizmi. (Klik voor een voorbeeld hier).

Antwoordblad

Stampioen

De Hisab al-jabr wal-moeqabala van Al-Chwarizmi werd in het Latijn vertaald en heeft zeer lang grote invloed gehad. In de zeventiende eeuw werd bijvoorbeeld in Nederland vierkantsvergelijkingen nog steeds volgens het meetkundige model van Al-Chwarizmi behandeld. In het boek Algebra ofte Nieuwe Stel-Regel van Stampioen uit 1639 komt bijvoorbeeld de volgende passage voor. Het gaat om de vergelijking x² + 4x = 60.

Oefening 3
a. Lees de tekst hieronder twee keer hardop. Stampioen gebruikt nog niet dezelfde schrijfwijze voor vergelijkingen als wij nu (deze werd door Descartes in 1637 ingevoerd, dus Stampioen had hem net kunnen kennen). Wat schreef hij voor x² en x? (Klik dit aan in de tekst hieronder).


b. Probeer stap voor stap te volgen wat er gebeurt. Teken de afbeelding over en zet letters en cijfers bij de zijden (eigenlijk begint het met vierkant AEFG). Schrijf in gewoon Nederlands wat Stampioen deed.

Antwoordblad

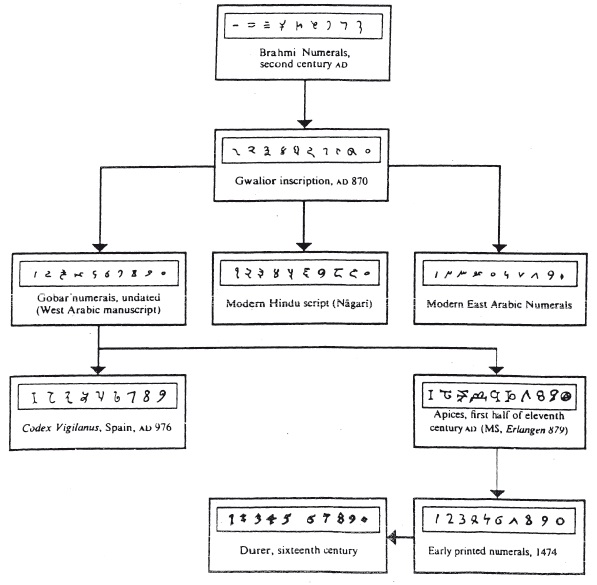
Het ontstaan van onze cijfers

Onze cijfers worden Hindu-Arabisch genoemd. Zoals je hieronder kunt zien zijn ze voor een deel herkenbaar in een inscriptie uit 870. In 1202 werden ze door Leonardo van Pisa (“Fibonacci“), die veel had gereisd, in zijn Boek over abacus in West-Europa geïntroduceerd. Het heeft daarna trouwens nog geruime tijd geduurd voordat ze gemeengoed geworden zijn.

Video – The Weird Truth About Arabic Numerals
In deze video wordt in het Engels uitgelegd hoe onze cijfers tot stand zijn gekomen. Ook wordt er vertelt wat Al-Chwarizmi hier mee te maken had (Engelse ondertiteling is mogelijk).

Tijdlijn – Geschiedenis van de wiskunde