Griekenland

Inhoudsopgave

Klik op de regel en je scrollt meteen naar het onderwerp in kwestie.

Inleiding

Hoewel er één Griekse wiskundige was die zich met name met algebra bezig hield (Diophantus), was de Griekse wiskunde sterk op meetkunde gericht. We zullen daarom vooral naar de meetkunde kijken.
Eerst zullen we twee van de drie klassieke problemen bestuderen

  1. De driedeling van de hoek
  2. De verdubbeling van de kubus
  3. De kwadratuur van de cirkel

De driedeling van een hoek

Figuur 3.1

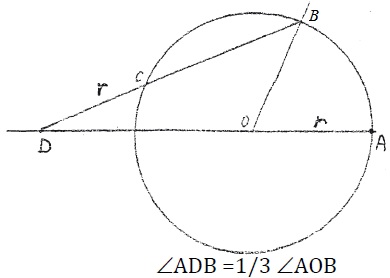
Oefening 1
Hoe bewijs je dat ∠ADB = 1/3 ∠AOB?
De driehoeken DCO, COB en BAO zijn gelijkbenige driehoeken.
Wanneer ik ∠ODC α noem, geldt ook ∠DOC = α.
a. Hoe groot is dan ∠DCO, uitgedrukt in α?
b. Nu is ∠BCO te berekenen. Hoe groot is deze, uitgedrukt in α?
c. Omdat driehoek COB gelijkbenig is, is ∠CBO gelijk aan ∠BCO, zodat ook ∠COB uit te rekenen is. Hoe groot ∠COB, uitgedrukt in α?
d. Hoe groot is ∠AOB, uitgedrukt in α?

Antwoordblad

Conchoïde

Je hebt in oefening 1 kunnen zien dat ∠ODC gelijk is aan 1/3 ∠AOB, en de driedeling van de hoek is dus mogelijk. Alleen ……. lijnstuk CD inpassen tussen de cirkel en lijn AO lukt niet als je alleen maar p&l mag gebruiken. De Grieken hadden dus andere teken- hulpmiddelen nodig, en voor het tekenen van lijn BCD hadden ze een apparaatje uitgevonden waarmee de constructie gemakkelijk uit te voeren was (maar natuurlijk niet op de door Euclides voorgeschreven manier, dus eigenlijk was het gebruik van zo’n apparaatje illegaal):
Het is een soort liniaal, die kan draaien rond een punt (hier G genoemd). Langs de liniaal kan een schuifje PQ heen en weer schuiven. Je kunt de lengte van het schuifje PQ zelf instellen. Kijk nu wat er gebeurt als je punt P van het schuifje langs de rechte lijn l laat bewegen terwijl er in Q een tekenstift zit.
De liniaal draait dus om G terwijl P de lijn l doorloopt. Je krijgt dan een kromme. Deze kromme heet de conchoïde.

Om een idee te krijgen hoe dit werkt, kun je onderstaande video bekijken:

Hieronder zie je een GeoGebra applet (gemaakt met de hulp van Karin Rinsma) van bovenstaande situatie. Wat gebeurt er als je P over de lijn beweegt (druk linksonder op play)? De lengte van PQ kun je linksboven veranderen.

Constructie van Nicomedes

Een andere constructie van de driedeling van de hoek kwam van Nicomedes (±225 v.Chr).
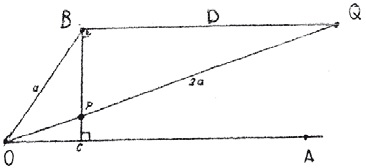
Hij zegt: ∠AOB is de gegeven hoek. Uit het punt B worden BC ⊥ OA en BD // OA getrokken.
De rechte OPQ wordt zo getrokken, dat PQ = 2 ⋅ OB met P op BC en Q op BD. Dan is ∠AOQ = 1/3 ∠AOQ α.

Pas in 1837 bewees de Franse wegen- en bruggenbouwer Pierre Louis Wantzel dat er geen algemene constructie is voor de driedeling van de hoek. Toch zijn er nog steeds mensen, die de hoop niet hebben opgegeven. In een berichtje in de krant van enige jaren geleden werd vermeld dat een inwoner van Düsseldorf meer dan 12000 uur had besteed aan het vinden van een constructie, die voor elke hoek werkt…

Quadratrix (van Hippias)

Hippias van Elis creëerde rond 420 v.Chr. de kromme om het probleem van de trisectie op te lossen. Het is een van de oudste dynamische krommen in de wiskunde: ze wordt gevormd door de meetkundige plaats van een bewegend punt en niet door een statische vergelijking. De definitie van de kromme mag dan wel merkwaardig zijn, eens de kromme gevormd, is de driedeling van een willekeurige hoek zeer eenvoudig. De kromme wordt niet trisectrix maar quadratrix genoemd omdat, rond 350 v.Chr., Dinostratus dezelfde kromme gebruikte om de kwadratuur van de cirkel te berekenen.

De kromme als meetkundige plaats
Een punt E beweegt op de cirkelboog met middelpunt A van D naar B. Tegelijk beweegt een punt F verticaal naar beneden vanuit C zo dat E en F tegelijk in B aankomen. De quadratrix is de meetkundige plaats van het punt P als snijpunt van de lijnstuken |AE| en |GF|.

 

De spiraal van Archimedes

Een Archimedes-spiraal ontstaat wanneer je een punt met constante snelheid laat bewegen langs een lijn die zelf met een constante snelheid ronddraait.

Trisectie met spiraal van Archimedes

Trisectie met spiraal van Archimedes – alternatief

Wil je de spiraal van Archimedes zelf construeren? Bekijk dan deze video.

De verdubbeling van de kubus

Hierboven zie je een Engelstalige video waarin het klassieke probleem van de verdubbeling van de kubus wordt uitgelegd. De Nederlandse uitleg volgt hieronder:

De Grieken echter moesten (of wilden) dit probleem meetkundig oplossen, en het liefst natuurlijk met passer en liniaal, en het is interessant om te zien hoe ze het hebben aangepakt.

Hippocrates had bedacht dat wanneer je er in zou slagen om tussen de lijnstukken a en 2a twee middelevenredigen te construeren, je de oplossing zou hebben (met passen en liniaal kun je uit a ook 2a krijgen).

Het plan van Hippocrates betekent in moderne notatie dat je de lijnstukken x en y zo moet construeren, dat a : x = x : y = y : 2a, x en y worden twee middelevenredigen tussen a en 2a genoemd. De eerste van deze twee, x, is dan de ribbe van de gezochte kubus.
NB In het algemeen noemen we x en y de middelevenredigen van a en b als geld: a : x = x : y = y : b
Bijvoorbeeld 6 en 18 zijn de middelevenredigen van 2 en 54 (x=6, y=18 en a=2, b=54):

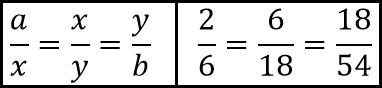
Stel dat inderdaad x en y geconstrueerd zijn waarvoor geldt a : x = x : y = y : 2a. Dan geldt:
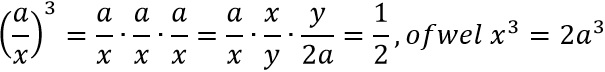Dus dan is x de zijde van de verdubbelde kubus.

Om het probleem op te lossen werd eerst een trapje lager gezocht:

Definitie: l heet de middelevenredige van k en m als geldt: k : l = l : m.
Bewering: het is mogelijk om met passer en liniaal de middelevenredige van twee willekeurige lijnstukken k en m te construeren.
Oplossing: Leg de lijnstukken k en m achter elkaar op een rechte lijn. Bepaal met passer en liniaal het midden Q van lijnstuk k + m. Noem het snijpunt van de halve cirkel en de loodlijn T. Dan is ST de middelevenredige van k en m.

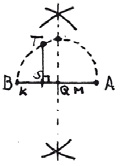
Hieronder in de GeoGebra Applet zie je bovenstaande verwerkt.

Oefening 2
a. Wat is de omgekeerde stelling van Thales?
b. Gebruik dit om aan te tonen dat de driehoeken SBT en STA gelijkvormig zijn.
c. Toon nu aan: k : ST = ST : m

Antwoordblad

Helaas bleek het construeren van twee middelevenredigen een even groot probleem te zijn als de driedeling van de hoek. De Grieken moesten hun toevlucht nemen tot het gebruik van andere krommen (dus anders dan lijn en cirkel) of van andere instrumenten dan passer en liniaal.
Er zijn verschillende oplossingen in die richting gevonden. Zo omvatten gecompliceerde methodes van het verdubbelen van de kubus de conchoïde van Nicomedes of de cissoïde van Diocles. Hieronder wordt de cissoïde van Diocles uitgewerkt.

De Cissoïde (van Diocles)

De kromme

  • Teken een cirkel met middelpunt M en teken een raaklijn in een punt B op de cirkel.
  • Teken een rechte door het punt O tegenover B en een punt A op de raaklijn.
  • Bepaal het snijpunt Q van deze rechte met de cirkel.
  • Bepaal het punt P zodat 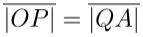De cissoïde is de meetkundige plaats van het punt P wanneer je A versleept op de raaklijn in B.


De Cissoïde als hulpmiddel om een kubus te verdubbelen

De kwadratuur van de cirkel

Hieronder wordt het constructie probleem ‘de kwadratuur van de cirkel’ uitgelegd in de Engelstalige video genaamd ‘Squaring the Circle’.

De vraag is of het mogelijk is om, met behulp van alleen passer en liniaal in een eindig aantal stappen een vierkant te construeren met exact dezelfde oppervlakte als een gegeven cirkel. Zoals je in het filmpje hierboven hebt kunnen zien is dat onmogelijk en dat is pas bewezen in 1882.

De Grieken moesten hun toevlucht nemen tot het gebruik van andere krommen (dus anders dan lijn en cirkel) of van andere instrumenten dan passer en liniaal. Er zijn verschillende oplossingen in die richting gevonden. Zo omvatten gecompliceerde methodes van de kwadratuur van een cirkel de quadratrix van Hippias of de spiraal van Archimedes

De gulden snede

De gulden snede is de verdeling van een lijnstuk in twee delen in een speciale verhouding. Bij de gulden snede verhoudt het grootste van de twee delen zich tot het kleinste, zoals het gehele lijnstuk zich verhoudt tot het grootste. Geven we het grootste aan met x en het kleinste deel met 1, dan is de verhouding van beide zo dat x : 1 = (x + 1) : x

Tenslotte nog wat opmerkingen over het begrip middelevenredige, met betrekking tot de gulden snede.

Euclides heeft aangegeven hoe een lijnstuk AB verdeeld dient te worden om de gulden snede te verkrijgen: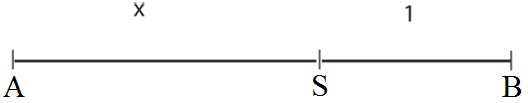

De waarde van φ wordt benaderd door de verhouding van twee opeenvolgende getallen in de rij van Fibonacci. Het quotiënt van twee opeenvolgende getallen uit die rij nadert, als we de rij tot in de oneindige uitbreiden, tot de guldensnedeverhouding.

Het gulden getal kan ook als kettingwortel worden uitgedrukt:

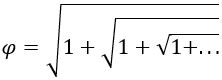
Een gulden rechthoek is een rechthoek met zijden in de verhouding van het gulden getal: lengte : breedte = φ

Als de breedte a is en de lengte a + b, geldt er:

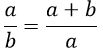
Als we in de gulden rechthoek een vierkant tekenen, met a als zijde, is de kleinere rechthoek die overblijft opnieuw een gulden rechthoek. Door dit proces met de steeds kleinere wordende rechthoeken te herhalen ontstaat een gulden spiraal (zie afbeelding hieronder).
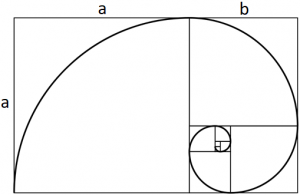Wil je zien hoe je een gulden spiraal kunt tekenen? Bekijk dan deze video.

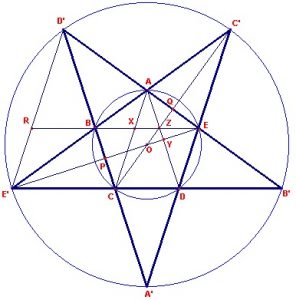
Het pentagram en φ

Het pentagram (vijfhoekige regelmatige ster) kan ontstaan door de zijden een regelmatige vijfhoek twee aan twee te verlengen.
We kiezen AB = 1 (de zijde van de regelmatige vijfhoek).
Zijn R en r opvolgend de stralen van de omgeschreven cirkels van A’B’C’D’E’ en ABCDE, dan kunnen we eenvoudig vinden:

 

(i) AD’ = φ
(ii) OP / r = φ / 2
(iii) OE’ / r = φ²
(iv) OP / OE’ / r = 2 ⋅ φ
(v) Een diagonaal zoals BE heeft lengte f.
(vi) Is X het snijpunt van twee diagonalen AC en BE, dan geldt:

  • EX / XB = φ
  • CX / XA = φ

 

Tijdlijn – Geschiedenis van de wiskunde