Inhoudsopgave
Inleiding
Eén van de belangrijkste en meest productieve wiskundigen van alle tijden was Leonhard Euler (1707 – 1783). Een beroemde ontdekking van Euler is de polyederstelling. Deze stelling gaat over gesloten veelvlakken en luidt:
H + Z = R + 2
Met
H: aantal hoekpunten
R: aantal ribben
Z: aantal zijvlakken van het veelvlak
Oefening 1
a. Controleer de stelling voor een kubus en voor een piramide met een vierkant grondvlak.
b. Zoek een meetkundig lichaam, dat door vlakken begrensd is, maar waarvoor de stelling van Euler niet geldt (hint: zoek een lichaam met een gat erin).
Oefening 2
a. Onderzoek of er veelvlakken zijn met 5 zijvlakken Teken ze, indien mogelijk.
b. Onderzoek of er veelvlakken zijn met 7 ribben. Teken ze, indien mogelijk.
Euler’s bewijs van deze stelling bleek later niet helemaal in orde te zijn. Voor de filosofen onder ons: er is een heel boek over geschreven door l. Lakatos (Proofs and Refutations).
In de Oudheid was veel studie gemaakt van regelmatige viervlakken. Er was toen al bekend dat er 5 regelmatige veelvlakken zijn. Je hebt in Berlinghoff kunnen lezen welke dit zijn.
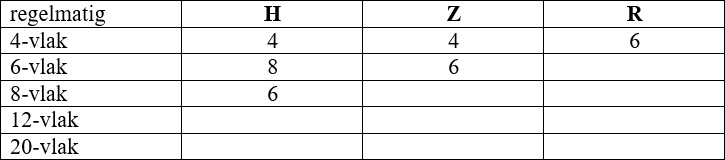
Oefening 3
Vul onderstaande tabel in (gebruik de stelling van Euler en de tekeningen in het boek van Berlinghoff):
Beschrijving Leonhard Euler
Op de website van Canon van de wiskunde staat ook een beschrijving over het leven van Leonhard Euler.
Wie was hij, waarom was (en is) hij belangrijk en wat is zijn bijdrage voor de wiskunde en de samenleving?
STELLING: Er bestaan niet meer regelmatige veelvlakken dan de vijf die we al kennen.
BEWIJS: In elk regelmatig veelvlak geldt de formule H + Z = R + 2.
Elke zijvlak is een regelmatige n-hoek, met n ≥ 3. Elk zijvlak wordt begrensd door n ribben; dit geeft in totaal Z ⋅ n ribben. Maar je telt zo elke ribbe twee keer, want elke ribbe ligt in twee zijvlakken. Er geldt dus (Z ⋅ n) ÷ 2 = R.
Noem nu het aantal ribben dat in een hoekpunt samenkomt a (voor elk hoekpunt is dit aantal hetzelfde!). Er geldt a ≥ 3.
Oefening 4
Waarom moeten n en a minstens 3 zijn?
De H hoekpunten leveren dus H ⋅ a ribben op. Maar ook nu weer wordt elke ribbe twee keer geteld (waarom?), zodat geldt (H ⋅ a) ÷ 2 = R.
Beschrijving Carl Friedrich Gauss
Toen de negentiende eeuw was begon, was Carl Friedrich Gauss (1777 – 1855) de dominante persoon in de wiskunde. Hij schijnt een wonderkind te zijn geweest, dat al kon rekenen toen hij drie was. Op zeventienjarige leeftijd deed hij al belangrijke nieuwe ontdekkingen, die hij in zijn wiskundige dagboek noteerde.
Op de website van Canon van de wiskunde staat ook een beschrijving over het leven van Carl Friedrich Gauss.
Wie was hij, waarom was (en is) hij belangrijk en wat is zijn bijdrage voor de wiskunde en de samenleving?
Wil je nog meer weten over Gauss? Bekijk dan deze video.
Reeksen
Al vanaf de middeleeuwen is er belangstelling geweest voor de harmonische reeks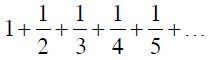 
We laten nu drie “bewijzen” zien dat deze reeks divergent is (dat wil zeggen dat de som boven elke grens uitstijgt, of eenvoudiger gezegd: dat de som oneindig is).
Nicole Oresme (1323 – 1382) is de eerste, die aan bod komt.
Oresmes redenering luidde als volgt:
Je kunt de reeks verdelen in een oneindig aantal groepen met termen die elk een som hebben die groter is dan ½:
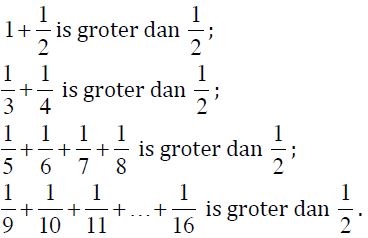Hieruit volgt dat de som van de totale reeks oneindig is.
Johann Bernoulli (1667 – 1748) had een andere redenering om hetzelfde aan te tonen. Die ging als volgt:
Als je nu bij alle reeksen ((3) + (4) + (5) + (6) + …..) de linkertermen sommeert door per kolom op te tellen, krijg je N.
Oefening 5
a. Waarom is dat zo?
b. Als je de rechtertermen optelt krijg je A. Waarom?
c. Je krijgt nu N = A. En dus moet A oneindig zijn, zegt Bernoulli. Wat vind jij?
Oefening 6
Bekijk onderstaande (Engelstalig) video over Euler’s Identity. In deze video zullen vragen voorbij komen over het geen wat je op deze website al hebt kunnen lezen. De eerste drie minuten komen er tijdens het kijken vragen voorbij. Daarna volgt er een stuk uitleg over Euler’s Identity. Dit is een erg interessant stuk over hoe e is gedefinieerd. Ook krijg je hier een indruk over hoe wiskundigen te werk gingen om nieuwe ontdekkingen te doen.
“The briljant thing about mathematicians is that when they on their way to some wonderful mathematical discovery, they don’t let a little thing like “numbers not existing” stop them. After all, matematics is the science of numbers, so if a number, rather inconveniently, doesn’t exist… Well, they just jolly wel go out and invent one.” – Mark Newman